Die Jensen Shannon Divergence wird verwendet, um die Ähnlichkeit zwischen zwei Wahrscheinlichkeitsverteilungen zu messen, insbesondere im Bereich des maschinellen Lernens. Hier erfährst du alles, was du über dieses Maß wissen musst, von seiner Geschichte bis hin zu seinen modernen Anwendungen!
Jahrhundert haben der dänische Mathematiker Johan Jensen und der amerikanische Statistiker Peter Shannon wichtige Beiträge zur Informationstheorie und zur Statistik geleistet.
Der 1859 geborene Johan Jensen widmete einen Großteil seiner Karriere der Untersuchung von konvexen Funktionen und Ungleichungen. Im Jahr 1906 veröffentlichte er einen Artikel mit dem Titel „Über konvexe Funktionen und Ungleichungen zwischen Mittelwerten“.
Darin führte er den Begriff der Konvexität ein und stellte mehrere Ergebnisse zu den nach ihm benannten Jensen-Ungleichungen auf. Dabei handelt es sich um mathematische Ergebnisse, die die Eigenschaften von konvexen Funktionen beschreiben.
Peter Shannon wurde 1917 geboren und beschäftigte sich lange Zeit mit Divergenzmaßen zwischen Wahrscheinlichkeitsverteilungen. Insbesondere beschäftigte er sich mit Problemen im Zusammenhang mit der Schätzung der Dichte.
In den 1940er Jahren, Jahrzehnte nach Jensens Arbeiten, entwickelte der Amerikaner Methoden zur Schätzung der Divergenz zwischen Wahrscheinlichkeitsverteilungen.
Er stützte sich dabei auf die Kullback-Leibler-Divergenz: ein Maß, das in den 1950er Jahren von Solomon Kulback und Richard Leibler erfunden wurde und weithin zur Quantifizierung der Differenz zwischen zwei Verteilungen verwendet wird.
Diese misst die Unähnlichkeit zwischen zwei Wahrscheinlichkeitsverteilungen, indem sie auf den Logarithmen der Wahrscheinlichkeitsverhältnisse basiert.
Später, in den 1990er Jahren, begannen Forscher, die Möglichkeiten von Erweiterungen und Variationen der Kullback-Leibler-Divergenz zu untersuchen.
Ihr Ziel war es, die Symmetrie und Unähnlichkeit von Verteilungen besser zu berücksichtigen. So ließen sie sich von den Vorarbeiten von Johan Jensen und Peter Shannon inspirieren und schufen die Jensen Shannon Divergence.
Was ist die Jensen Shannon Divergence?
Die Jensen Shannon Divergence wurde erstmals 1991 von Barry E. S. Lindgren in einem Artikel mit dem Titel „Some Properties of Jensen-Shannon Divergence and Mutual Information“ eingeführt.
Er entwickelte diese Metrik als Maß für die symmetrische Divergenz zwischen zwei Wahrscheinlichkeitsverteilungen. Ihr Hauptunterschied zur Kullback-Leibler-Divergenz, auf der sie basiert, ist die Symmetrie.
Sie nimmt den gewichteten Mittelwert zweier KL-Divergenzen. Eine wird aus der ersten Verteilung berechnet, die andere aus der zweiten.
Man kann also die Jensen Shannon Divergence als gewichtetes Mittel der Kullback-Leibler-Divergenzen zwischen jeder Verteilung und einer Durchschnittsverteilung definieren.
Wie berechnet man die Jensen Shannon Divergence?
Der erste Schritt zur Berechnung der Jensen-Shannon-Divergenz besteht darin, die Daten vorzuverarbeiten, um die Wahrscheinlichkeitsverteilungen P und Q zu erhalten.
Anschließend können die Wahrscheinlichkeitsverteilungen aus den Daten geschätzt werden. Es ist z. B. möglich, das Auftreten jedes Elements in der Stichprobe zu zählen.
Wenn die Verteilungen verfügbar sind, kann man die Divergenz mit der Formel :
JS(P || Q) = (KL(P || M) + KL(Q || M)) / 2
wobei M = (P + Q) / 2 und || den Verkettungsoperator darstellt.
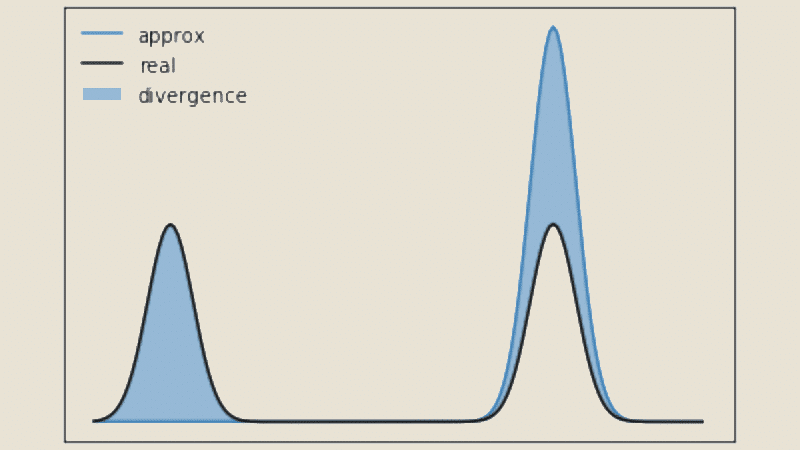
Ein höherer Wert der JS-Divergenz deutet auf eine größere Unähnlichkeit zwischen den Verteilungen hin, während ein Wert, der näher bei Null liegt, eine größere Ähnlichkeit anzeigt.
Um dies an einem konkreten Beispiel zu verdeutlichen, nehmen wir an, dass wir zwei Texte haben und ihre Ähnlichkeit messen wollen.
Jeder Text kann durch eine Verteilung von Wörtern dargestellt werden, wobei jedes Wort ein Element des Alphabets ist.
Indem wir die Vorkommen der Wörter in jedem Text zählen und diese Vorkommen durch die Häufigkeit der Gesamtheit der Wörter normalisieren, erhalten wir die Wahrscheinlichkeitsverteilungen P und Q.
Anschließend verwenden wir die Jensen-Shannon-Divergenzformel, um einen Wert zu berechnen, der angibt, wie ähnlich sich die beiden Texte sind!
Bei diesem Maß sind mehrere wichtige Eigenschaften hervorzuheben. Zunächst einmal ist sie immer positiv und erreicht nur dann den Wert Null, wenn die Verteilungen P und Q identisch sind.
Außerdem ist sie durch log2(n) nach oben begrenzt, wobei n die Größe des Alphabets der Verteilung ist. Sie ist statistisch signifikant und kann in Hypothesentests und Konfidenzintervallen verwendet werden.
Vor- und Nachteile
Die Stärke der Jensen Shannon Divergence ist, dass sie die globale Struktur der Verteilungen berücksichtigt. Sie ist daher resistenter gegen lokale Variationen als andere Divergenzmaße.
Ihre Berechnung ist relativ effizient, was sie außerdem für große Datenmengen anwendbar macht. Dies sind ihre Hauptvorteile.
Andererseits kann sie empfindlich auf die Größe der Stichproben reagieren. Die Schätzungen der Wahrscheinlichkeitsverteilungen können bei kleinen Stichprobengrößen unzuverlässig sein, was sich auf das Ähnlichkeitsmaß auswirken kann.
Sie kann auch weniger geeignet sein, wenn die Verteilungen sehr unterschiedlich sind. Der Grund dafür ist, dass sie nicht die feinen Details der lokalen Unterschiede erfasst.
Jensen Shannon Divergence und Machine Learning
Im Bereich des maschinellen Lernens spielt die JS-Divergenz eine entscheidende Rolle. Sie misst die Ähnlichkeit zwischen den Wahrscheinlichkeitsverteilungen, die mit verschiedenen Stichproben oder Clustern verbunden sind.
Sie kann verwendet werden, um ähnliche Daten zusammenzufassen oder um neue Stichproben durch Vergleich mit Referenzverteilungen zu klassifizieren.
Bei der Verarbeitung natürlicher Sprache kann man sie verwenden, um die Verteilungen von Wörtern in verschiedenen Texten zu vergleichen. Dadurch lassen sich ähnliche Dokumente identifizieren, doppelte Inhalte aufspüren oder semantische Beziehungen zwischen Texten finden.
Es ist auch ein Werkzeug zur Bewertung von Sprachmodellen. Insbesondere kann man es nutzen, um die Vielfalt und Qualität der erzeugten Texte zu bewerten.
Indem man die Wahrscheinlichkeitsverteilungen der erzeugten Texte mit denen der Referenztexte vergleicht, kann man messen, wie ähnlich oder unterschiedlich die Generationen dem Referenzkorpus sind.
In Fällen, in denen die Lern- und Testdaten aus unterschiedlichen Verteilungen stammen, kann die Jensen-Shannon-Divergenz verwendet werden, um die Strategien zur Domänenanpassung zu lenken.
Dies kann dabei helfen, ein Modell, das auf einer Quellverteilung trainiert wurde, so anzupassen, dass es sich besser an die neuen Daten einer Zielverteilung anpasst.
Schließlich kann für die Sentimentanalyse die JS-Divergenz verwendet werden, um die Profile zwischen verschiedenen Dokumenten oder Musterklassen zu vergleichen.
Dadurch können Ähnlichkeiten und Unterschiede im Ausdruck identifiziert werden, z. B. bei der Erkennung von Meinungen oder der Klassifizierung von Emotionen.
💡Auch interessant:
Jensen Shannon Divergence und Data Science
In der Datenwissenschaft dient die JS-Divergenz dazu, die Ähnlichkeit zwischen den Verteilungen von Variablen oder Merkmalen in einem Datensatz zu vergleichen.
Sie kann verwendet werden, um den Unterschied zwischen beobachteten Datenverteilungen und erwarteten oder Referenzverteilungen zu messen.
Dadurch können Variationen und Abweichungen zwischen den verschiedenen Verteilungen identifiziert werden, was für die Erkennung von Anomalien oder die Validierung von Hypothesen wertvoll sein kann.
Bei der Analyse von Textdaten kann damit die Ähnlichkeit zwischen Verteilungen von Wörtern, Sätzen oder Themen in Dokumenten geschätzt werden.
Dies kann dabei helfen, ähnliche Dokumente zu gruppieren, gemeinsame Themen zu extrahieren oder signifikante Unterschiede zwischen Dokumentensätzen zu erkennen.
Es kann z. B. für die Klassifizierung von Dokumenten auf der Grundlage ihres Inhalts oder für die Stimmungsanalyse durch den Vergleich von Stimmungsverteilungen zwischen verschiedenen Texten verwendet werden.
Wenn es eine große Dimensionalität in den Daten gibt, kann die Jensen Shannon Divergence verwendet werden, um die am stärksten diskriminierenden Merkmale auszuwählen oder die Dimensionalität der Daten zu reduzieren.
Durch die Berechnung der Divergenz zwischen den Verteilungen verschiedener Merkmale können diejenigen Merkmale identifiziert werden, die am meisten zur Differenzierung zwischen Klassen oder Gruppen in den Daten beitragen.
Modellbewertung: Im Prozess der Entwicklung und Bewertung von Vorhersagemodellen kann die JS-Divergenz als Metrik verwendet werden, um die Wahrscheinlichkeitsverteilungen der Vorhersagen und der tatsächlichen Werte zu vergleichen.
Dies ermöglicht es, die Qualität des Modells zu bewerten, indem gemessen wird, wie gut die Vorhersagen mit den tatsächlichen Beobachtungen übereinstimmen.
Beispielsweise kann sie bei der Bewertung von Klassifikations-, Regressions- oder Empfehlungsmodellen eingesetzt werden.
Schließlich kann sie auch verwendet werden, um die Ähnlichkeit zwischen Beobachtungen oder Instanzen in einem Datensatz zu messen.
Indem man die Merkmalsverteilungen zwischen den verschiedenen Instanzen vergleicht, kann man die Nähe oder Distanz zwischen ihnen bestimmen. Dies kann in Clustering-Aufgaben verwendet werden, um ähnliche Beobachtungen zusammenzufassen oder um große Datenbanken nach Ähnlichkeiten zu durchsuchen.
Fazit: Die Jensen Shannon Divergence, ein Schlüsselwerkzeug für Datenanalyse und maschinelles Lernen
Seit ihrer Entstehung wurde die Jensen Shannon Divergence in vielen Bereichen eingesetzt, u. a. in der Informatik, der Statistik, der Verarbeitung natürlicher Sprache, der Bioinformatik und dem maschinellen Lernen.
Sie ist auch heute noch ein wichtiges Werkzeug zur Messung der Ähnlichkeit von Wahrscheinlichkeitsverteilungen und hat neue Möglichkeiten für die Datenanalyse und die statistische Modellierung eröffnet.
Forscher auf der ganzen Welt nutzen es, um Klassifizierungs- oder Clusteringprobleme zu lösen. Sie ist ein Schlüsselelement im Werkzeugkasten von Wissenschaftlern und Praktikern in vielen Bereichen, angefangen bei der Data Science.
Um zu lernen, alle Techniken der Analyse und des Machine Learning zu beherrschen, kannst du dich für DataScientest entscheiden.
In unseren Kursen kannst du alle Fähigkeiten erwerben, die du brauchst, um Dateningenieur, Analyst, Data Scientist, Data Product Manager oder ML-Ingenieur zu werden.
Du lernst die Programmiersprache Python und ihre Bibliotheken, DataViz-Tools, Business Intelligence-Lösungen und Datenbanken kennen.
Alle unsere Fortbildungen werden vollständig im Fernunterricht durchgeführt, ermöglichen den Erwerb einer beruflichen Zertifizierung und sind für die Finanzierung durch den Bildungsgutschein zugelassen. Entdecke DataScientest!