On dit qu’un modèle possède la propriété de Markov si son état à un instant T dépend uniquement de son état à l’instant T-1.
Si on peut observer les états dans lesquels se trouve le modèle à chaque instant, on parle de modèle de Markov observable. Sinon, on parle de modèle de Markov caché.
Dans cet article, nous allons illustrer ces modèles pour comprendre leur fonctionnement et leur utilité.
Modèle de Markov observable
Considérons la situation qui suit :
Vous êtes enfermés chez vous un jour de pluie, et vous aimeriez déterminer le temps qu’il fera lors des cinq prochains jours.
Comme vous n’êtes pas météorologue, vous vous simplifiez la tâche en faisant l’hypothèse que la météo suit un modèle de Markov: le temps qu’il fait au jour J dépend uniquement du temps qu’il fait au jour J-1.
Pour simplifier encore plus, vous considérez qu’il y a seulement trois temps possibles: soleil, nuages ou pluie.
En se basant sur les observations des derniers mois, vous établissez le diagramme de transitions suivant :
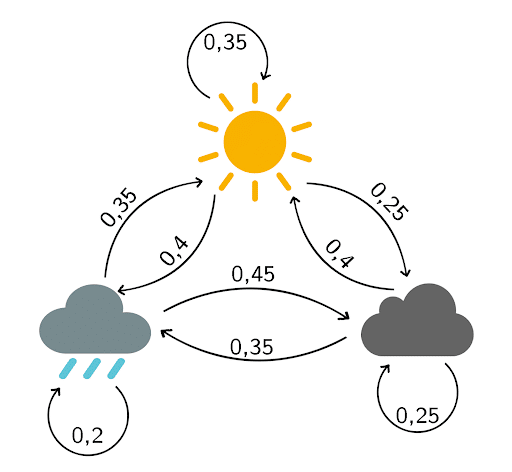
La matrice de transition associée est
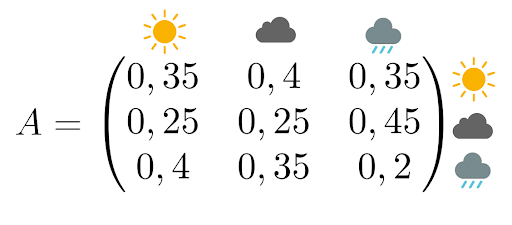
Pour rappel, cette matrice se lit de cette manière :
- La probabilité qu’il fasse beau demain sachant qu’il pleut aujourd’hui est de 35%
- La probabilité qu’il y ait des nuages demain sachant qu’il y en a déjà aujourd’hui est de 25%
Calculons la probabilité que le temps des cinq prochains jours soit “soleil, soleil, pluie, nuages, soleil”.
Comme le temps d’un jour dépend uniquement du temps qu’il a fait la veille, il suffit de multiplier les probabilités (pour rappel il pleut aujourd’hui):
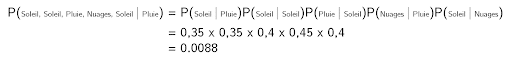
On peut calculer cette probabilité pour toutes les combinaisons possibles, et sélectionner la combinaison avec la probabilité la plus grande pour répondre à la problématique.
Dans notre cas, voici les 5 combinaisons qui ont le plus de chance d’être réalisées :
Modèle de Markov caché
On garde les mêmes hypothèses que dans la partie précédente.
Supposons maintenant qu’un psychopathe de la météo vous a enfermé dans une pièce sans fenêtre avec seulement un ordinateur et une lampe. Chaque jour, la lampe s’allume d’une certaine couleur en fonction de la météo. Votre kidnappeur vous fournit la matrice d’observation suivante :
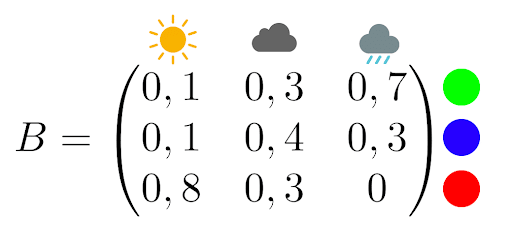
Par exemple s’il pleut, la lampe a 70% de chances d’être verte et 30% de chances d’être bleue.
Vous pourrez rentrer chez vous si vous déterminez le temps qu’il fera lors des cinq prochains jours uniquement en vous basant sur la couleur de la lampe. Vous construisez alors un modèle de Markov caché.
Vous restez enfermé 5 jours et vous relevez les couleurs suivantes:
bleu, bleu, rouge, vert, rouge.
Vous vous souvenez qu’il pleuvait le jour précédant votre enfermement
Vous pouvez alors rédiger un code python qui renvoie la combinaison qui a la plus forte probabilité d’être réalisée :
NB : On aurait également pu implémenter l’algorithme de Viterbi, qui aurait renvoyé la combinaison la plus probable, soit [‘Nuages’, ‘Nuages’, ‘Soleil’, ‘Pluie’, ‘Soleil’].
Cette approche de prédiction est intéressante mais très sommaire. Si vous voulez apprendre à faire des prédictions plus impressionnantes, avec des algorithmes de machine learning par exemple, contactez-nous directement en ligne pour avoir plus d’informations sur nos formations en data science !
