Une série temporelle ou série chronologique est un tableau de données traduisant l’évolution d’une variable dans le temps. Dans Python, celle-ci est souvent traitée sous la forme d’une Series Pandas indexée par un DateTime. Ce format permet une facilité de traitement et de visualisation très agréable.
Les séries temporelles sont utilisées dans de nombreux domaines tels que l’astronomie et la météorologie, mais sont probablement le plus utilisées en économie. On peut penser, par exemple, au cours des actions des entreprises ou encore à l’évolution des températures au cours du temps.
Le processus ARMA
AR
Une première modélisation des séries temporelles peut se faire en utilisant le modèle AR ou auto-régressif. Ce modèle vise à prédire la valeur de notre série temporelle en un instant t à l’aide d’une somme sur les p instants précédents.
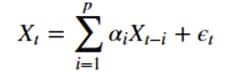
où on a :
- Xt la valeur à un instant t
- epsilon t l’erreur à un instant t
- alpha i le coefficient associé à Xt-i
MA
Le processus MA ou moving average quant à lui vise à prévoir la valeur à un instant t à partir des erreurs des q derniers instants.
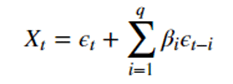
où on a :
- Xt la valeur à un instant t
- epsilon t l’erreur à un instant t
- beta i le coefficient associé à epsilon t-i
ARMA
Le processus ARMA combine un processus AR et un processus MA. On le note ARMA(p, q). La formule mathématique exacte est la suivante :
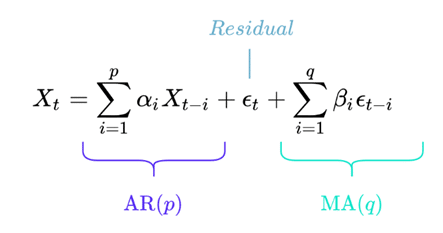
Avec les mêmes notation que précédemment.
Si cette formule peut faire peur, elle est en réalité très simple à comprendre.
Concrètement, un processus ARMA(1, 1) correspond à
Limites du modèle
Ce modèle, bien que très simple et donnant de bons résultats, a quelques limites. Tout d’abord, celui-ci ne donne de bons résultats que sur des séries temporelles dites stationnaires, c’est-à-dire dont la moyenne et la variance sont constantes.
De plus, il est difficile de prédire les prochaines valeurs à plus que t + 1 puisqu’on n’a alors plus de retour sur l’erreur de notre modèle pour la partie MA.
Etude en Python
Première analyse
Pour commencer notre analyse de la série temporelle, on importe la librairie Pandas ainsi que Matplotlib qui servira pour la visualisation et on lit le fichier csv dans lequel est stockée la série temporelle.
Dans cette ligne de commande, outre le nom du fichier à lire, les arguments de la fonction sont :
- parse_dates : cette argument indique à pandas que le Dataframe contient une colonne de dates et que celle-ci est la première colonne
- index_col : indique que l’index est également la première colonne
- squeeze : permet de renvoyer une Series et non un Dataframe
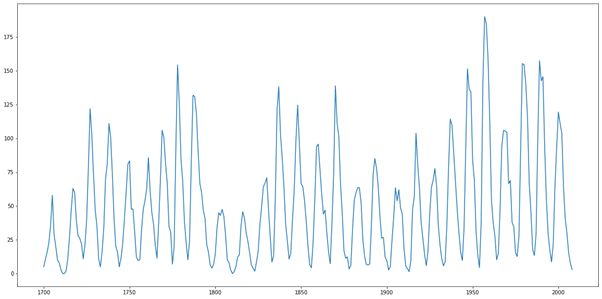
Pour commencer notre analyse, on peut visualiser notre série temporelle très simplement à l’aide de la bibliothèque matplotlib.pyplot en utilisant la fonction suivante :
Grâce à cette fonction, on obtient un graphique de l’évolution de notre variable au cours du temps.
Test de stationnarité
On procède ensuite à un test de stationnarité. Le test de Dickey-Fuller donne de bons résultats rapidement et est déjà implémenté dans Python dans la librairie Statsmodels.
En important la fonction et en l’utilisant de la manière suivante, on peut déterminer si notre série temporelle peut être modélisée par un processus ARMA :
Ce bout de code permet de récupérer la p-value du test de Dickey-Fuller de la série. Ce score indique si la série peut être considérée comme stationnaire. En général, s’il est inférieur à 0.05, on la considère stationnaire. Ici, notre p-value est de 0,053, nous sommes donc à la limite de la stationnarité car la variance de la série n’est pas vraiment constante, mais vous verrez que cela ne pose pas de problème par la suite.
Modélisation
On passe désormais à la modélisation de la série temporelle, qui va passer par la création d’un modèle ARMA dont il faudra ajuster les paramètres afin de correspondre le mieux possible à la série temporelle concernée, ce qui peut s’avérer difficile.
Ici, les termes p et q correspondent respectivement au premier et au dernier chiffres de l’argument order de la fonction. La méthode fit ajoutée à la fin sert à entraîner le modèle pour qu’il détermine seul ses paramètres.
La méthode summary permet de vérifier que notre modèle est bon, elle affiche :
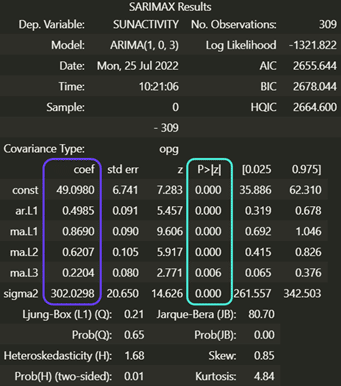
Ce tableau peut paraître impressionnant, mais il est en réalité très simple à interpréter. La colonne colonne entourée en violet correspond aux paramètres du modèle et la colonne en bleu donne la p-value de chacun des paramètres. Ici on voit que les paramètres sont bons car la p-value est toujours inférieure à 0,05. Si ce n’est pas le cas, on peut modifier p et q pour supprimer les paramètres inutiles.
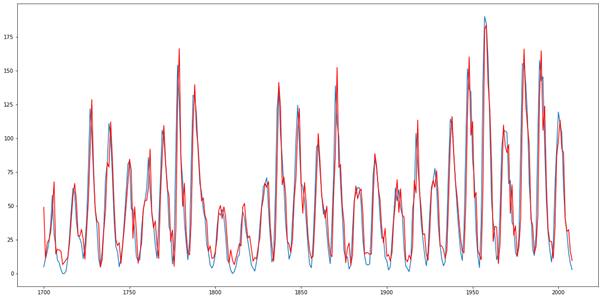
On accède aux résultats et on les visualise en faisant :
On a ainsi en rouge notre modèle et en bleu les valeurs réelles :
Conclusion
En conclusion, on est arrivés à modéliser notre série temporelle, mais notre modèle possède des limites que nous avons abordées plus haut. Pour traiter des séries temporelles non stationnaires, on pourra utiliser le modèle ARIMA qui ajoute une différentiation.. Si notre série présente une saisonnalité, c’est-à-dire des variations à un intervalle de temps régulier, il faudra plutôt utiliser le modèle SARIMA. Ces modèles et plus encore sont abordés dans notre cursus de Data Scientist.