Das war's! Der Datensatz ist bereinigt! Es gibt keine fehlenden Werte mehr, die Modellierungsentscheidungen wurden getroffen! Wir haben einige Variablen beibehalten und andere entfernt. Jetzt müssen wir den letzten Schritt vor dem Einsatz von Machine-Learning-Algorithmen machen: die Variablen scannen bzw. sie an den Algorithmus anpassen.
Die meisten Machine-Learning-Algorithmen erlauben es nicht, andere als numerische Variablen zu verwenden: Abgesehen von Entscheidungsbäumen und ihren Ableitungen (Zufallswälder, Gradient Boosting Tree usw.) beruhen die am häufigsten verwendeten Machine-Learning-Algorithmen auf der Berechnung von Abständen zwischen verschiedenen Beobachtungen.
In diesem Artikel beschäftigen wir uns damit, wie man Daten für einen Machine-Learning-Algorithmus aufbereitet und wie man Variablen scannen kann.
Variablen scannen - Eine quantitative Variable vorbereiten
Wenn man Machine Learning betreibt, stößt man sehr schnell auf quantitative Variablen: das Alter eines Kunden, der Preis eines Autos, die Fläche eines Grundstücks…. Es gibt übrigens letztendlich nur wenige Unterschiede zwischen einer diskreten und einer kontinuierlichen Variable: Die Transformationen, die wir an ihnen vornehmen, haben keinen Einfluss auf die Qualität der enthaltenen Informationen.
Um eine quantitative Variable aufzubereiten, wird eine Standard- oder Min-Max-Normierung verwendet. Diese Normalisierung bringt die Werte in einen normalisierten Bereich: 0 bis 1 für Min-Max und -1 bis 1 für die meisten Daten für Standard.
Eine der Hauptfunktionen der Datennormalisierung ist die Verbesserung und Beschleunigung der Konvergenz von Algorithmen, die auf dem Gradientenabstieg basieren (SVMs, Regressionen…), aber sie kann auch zu relevanteren Ergebnissen beim Clustering führen: Im folgenden Beispiel werden Zufallsdaten erzeugt, wobei versucht wird, recht anschauliche Cluster und etwas ausreißerischere Daten zu definieren. Anschließend wird ein KMeans mit oder ohne Normalisierung durchgeführt:
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
%matplotlib inline
a = np.random.normal(size=100)
a[:50] = a[:50] + 100
a[50] = a[50] + 60
a[51] = a[51] + 40
b = np.random.normal(size=100)
b[25:75] = b[25:75] + 10
b[51] = b[51] - 10
df = pd.DataFrame({'a': a, 'b':b})
df_standard = df.copy(deep=True)
df_minmax = df.copy(deep=True)
df['cluster'] = KMeans(n_clusters=4).fit_predict(df)
df_standard[df_standard.columns] = StandardScaler().fit_transform(df_standard)
df_standard['cluster'] = KMeans(n_clusters=4).fit_predict(df_standard)
df_minmax[df_minmax.columns] = MinMaxScaler().fit_transform(df_minmax)
df_minmax['cluster'] = KMeans(n_clusters=4).fit_predict(df_minmax)
fig, axes = plt.subplots(ncols=3, nrows=2, figsize=(15, 10))
axes[0, 0].scatter(df['a'], df['b'], color='b', alpha=.5)
axes[0, 1].scatter(df_standard['a'], df_standard['b'], color='b', alpha=.5)
axes[0, 2].scatter(df_minmax['a'], df_minmax['b'], color='b', alpha=.5)
axes[0, 0].set_title('No scaler')
axes[0, 1].set_title('Standard scaler')
axes[0, 2].set_title('MinMax scaler')
Du erhältst eine Abbildung, die der folgenden ähnlich ist:
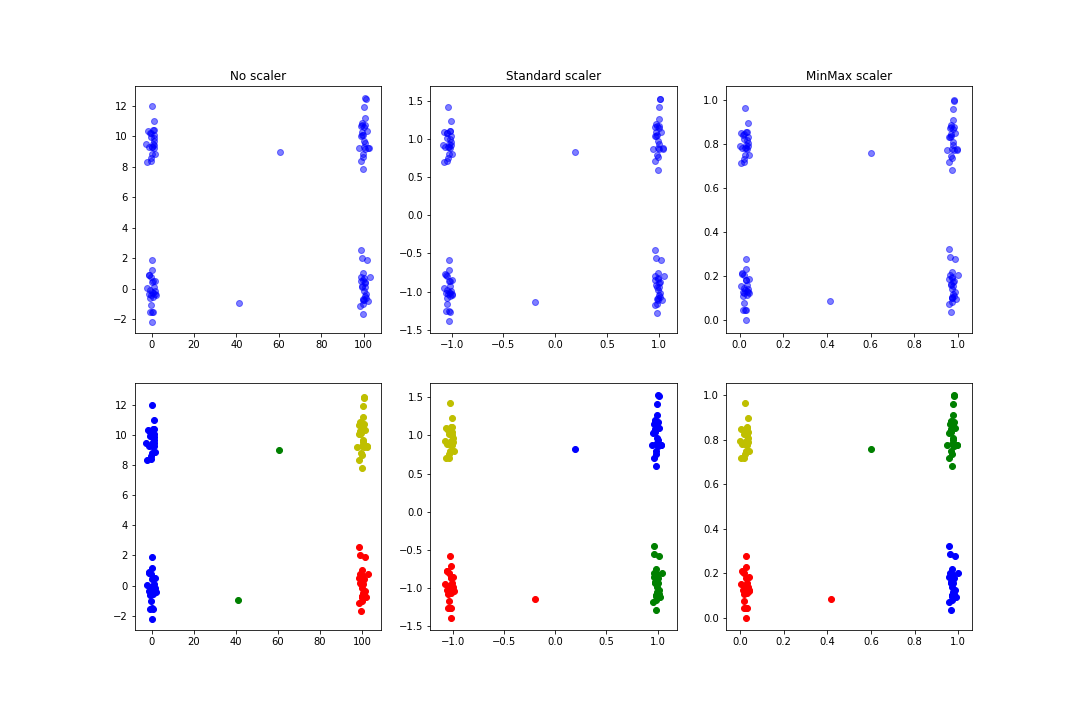
Man sieht, dass die gefundenen Cluster im Fall der Normalisierung logischer sind als im Fall vor der Normalisierung.
Der Hauptunterschied zwischen der Standardnormalisierung und der Min-Max-Normalisierung liegt in den Fällen, in denen extreme Werte gefunden werden. Bei der Standardnormalisierung wird eine Normalverteilung der Variablen angenommen, um die Werte für die Mehrheit zwischen -1 und 1 zu reduzieren. Im folgenden Beispiel hat die Variable b einige extreme Werte. Es fällt auf, dass die Normalisierung die Werte nicht auf dieses Intervall reduziert:
a = np.random.normal(loc=0, scale=2, size=1000)
a[:500] = a[:500]
b = a.copy()
b[:20] = b[:20] + 10
df = pd.DataFrame({'a': a, 'b': b})
df_standard = df.copy(deep=True)
df_minmax = df.copy(deep=True)
df_standard[df_standard.columns] = StandardScaler().fit_transform(df_standard)
df_minmax[df_minmax.columns] = MinMaxScaler().fit_transform(df_minmax)
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(20, 15))
axes[0, 0].hist(df['a'], bins=100, color='b')
axes[0, 1].hist(df_standard['a'], bins=100, color='r')
axes[0, 2].hist(df_minmax['a'], bins=100, color='g')
axes[0, 0].set_title('No scaler')
axes[0, 1].set_title('Standard scaler')
axes[0, 2].set_title('MinMax scaler')
axes[0, 0].set_ylabel('a')
axes[1, 0].set_ylabel('b')
axes[1, 0].hist(df['b'], bins=100, color='b')
Du erhältst eine Abbildung, die der folgenden ähnlich ist:
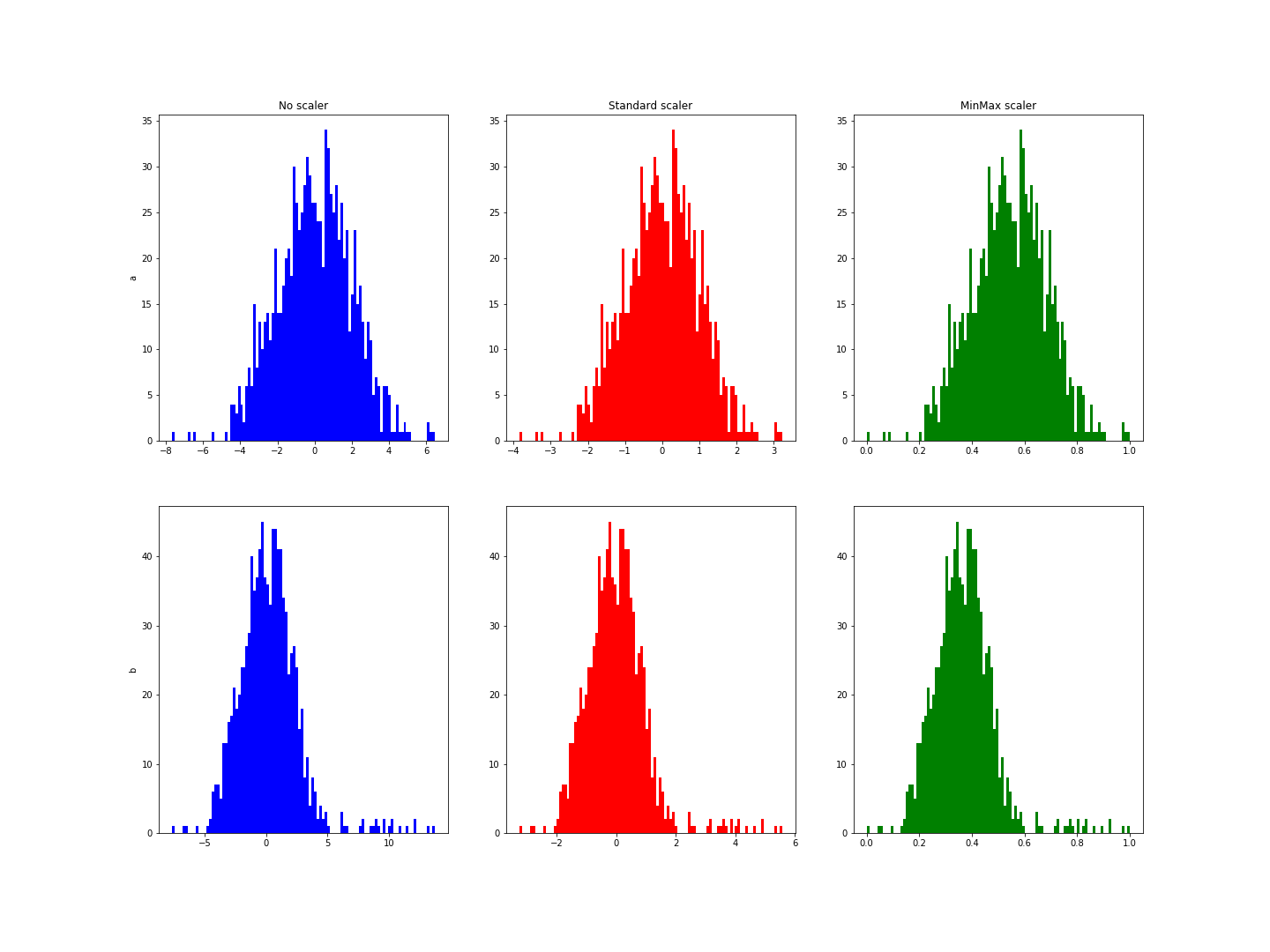
Diese Histogramme zeigen einen Bereich von -3 bis 6 für die Variable b, während der Bereich für a von -3 bis 3 reichte.
Natürlich haben wir in beiden Fällen absichtlich Ausreißer hinzugefügt, um den Effekt zu verstärken. In einem Data-Science-Projekt wären diese Werte früher entfernt worden, aber diese Beispiele geben eine Vorstellung davon, was Normalisierung für quantitative Variablen leisten kann.
Eine qualitative Variable vorbereiten
Es wurde bereits erwähnt, aber Machine-Learning-Algorithmen nehmen keine nicht-numerischen Variablen als Eingabe (zumindest nicht für Python und scikit-learn). Daher müssen diese Daten umgewandelt werden. Auch hier muss zwischen mehreren Fällen unterschieden werden.
Wenn es eine klare Hierarchie zwischen den verschiedenen Modalitäten gibt, dann kann man wahrscheinlich auf eine quantitative Variable zurückgreifen: Wenn zum Beispiel eine unserer Variablen eine Note von A bis F ist, dann muss man diese Noten auf Werte zwischen 0 und 20 zurückführen können, wobei F < E < D < C < B < A ist. Bei Produkten, die auf einer E-Commerce-Website angeboten werden, könnte neu 20, gut 15, mäßig 10, beschädigt 7, … sein. In diesem Fall genügt es, auf den vorherigen Absatz zu verweisen.
Aber wenn es keine Hierarchie gibt, was ist dann das Problem, dieselbe Art von Signatur zu verwenden? Wenn ich z. B. einen Datensatz mit Automodellen betrachte und die Variable Farbe mit drei Modalitäten (z. B. blau, rot und grün) habe: Wenn ich den Farben die Codes 0, 1 und 2 zuweise, dann erkenne ich, dass blau < rot < grün ist, was sehr fragwürdig ist! Mathematisch gesehen würde dies bedeuten, dass Blau + Blau = Blau ist, was bis jetzt ziemlich richtig ist, aber auch, dass Blau + Rot = Rot ist, was langsam lästig wird, und schließlich, dass Rot + Rot = Grün ist, was nur bei Farbenblindheit zutrifft!
Ein weiteres Problem ist, dass der Unterschied zwischen Blau und Grün doppelt so groß ist wie zwischen Blau und Grün, was wiederum fragwürdig ist.
df = pd.DataFrame({'couleur': ['bleu', 'rouge', 'vert']})
# encoder avec 0, 1, 2
code = {'bleu': 0, 'rouge': 1, 'vert': 2}
df_1 = df.copy(deep=True)
df_1['couleur'] = df_1['couleur'].apply(lambda c: code.get(c))
print(df_1.head())
from scipy.spatial import distance_matrix
import seaborn as sns
print('\nMatrices de distance')
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_1, df_1), annot=True)
plt.show()
In diesem Beispiel wird deutlich, dass der Abstand zwischen den Beobachtungen, die den Farben blau und grün entsprechen, größer ist als zwischen den Beobachtungen, die den Farben blau und rot oder rot und grün entsprechen.
Statt einer Variable haben wir drei Variablen mit jeweils 0 und 1: In der roten Spalte sind nur die Beobachtungen, die roten Fahrzeugen entsprechen, 1…
df_2 = df.copy(deep=True)
df_2 = pd.get_dummies(df_2)
print(df_2.head())
print('\nMatrices de distance')
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_2, df_2), annot=True)
plt.show()
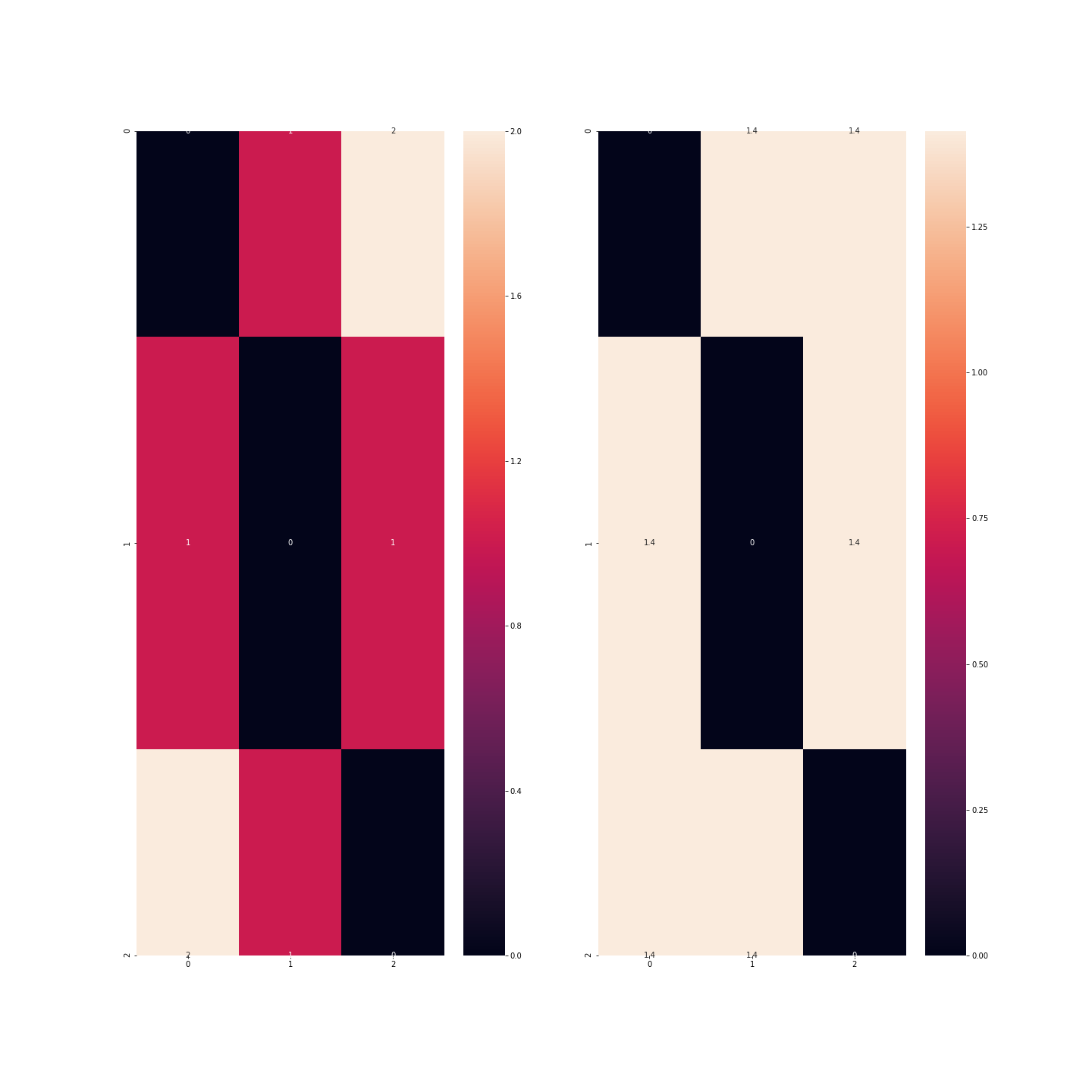
Es gibt jedoch einen Punkt, auf den wir in dieser Geschichte zurückkommen müssen: Wenn wir so viele Spalten wie Modalitäten nehmen, dann ist die Information in meinem Datensatz redundant. Wir können also auf eine dieser Modalitäten verzichten, da sie von den anderen Modalitäten impliziert wird, die dann alle null sind: Diese Technik ermöglicht es, den Datensatz zu verschlanken, aber vor allem eine Variable zu entfernen, die zu stark mit den anderen korreliert ist: Wenn es viele Modalitäten gibt, dann werden die meisten Indikatoren dieser Variablen für viele Beobachtungen null sein und sie werden gleichzeitig null sein.
Es gibt jedoch noch eine Kategorie, die wir erwähnen müssen: zirkuläre Variablen.
💡Auch interessant:
| Machine Learning Clustering: CAH Algorithmus |
| Deep Learning vs. Machine Learning |
| Data Poisoning |
| Machine Learning Data Sets Top 5 |
| Die Top 3 Machine Learning Algorithmen |
Eine zirkuläre Variable vorbereiten
Eine zirkuläre Variable ist eine quantitative oder qualitative Variable, die in sich geschlossen ist: die Monate des Jahres, die Tageszeit, die Jahreszeiten, das Lebensstadium eines Produkts, das unendlich oft recycelt werden kann, … Das Besondere an diesen Variablen ist, dass man eine Hierarchie zwischen den verschiedenen Werten definieren kann, dass diese Hierarchie aber zirkulär ist: 1 Uhr morgens wäre größer als 0 Uhr, genauso wie 0 Uhr größer als 23 Uhr wäre; ebenso wäre Frühling < Sommer < Herbst < Winter < Frühling < …
Du musst also einen Weg finden, diese Daten zu kodieren, ohne dabei zu viel Sinn zu verlieren. Bisher werden diese Daten als Zahlen von 0 bis 23 dargestellt.
df = pd.DataFrame({'heure': [i for i in range(24)]})
print(df.head())
Wenn wir dieses Format beibehalten, haben wir die Distanz zwischen 23:00 und 0:00 Uhr, die 23 Mal so groß ist wie die Distanz zwischen 0:00 und 1:00 Uhr. Im Gegenteil, das Verhalten einer Person um 23 Uhr, um Mitternacht oder um 1 Uhr morgens ist sehr ähnlich.
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df, df), annot=True)
plt.show()
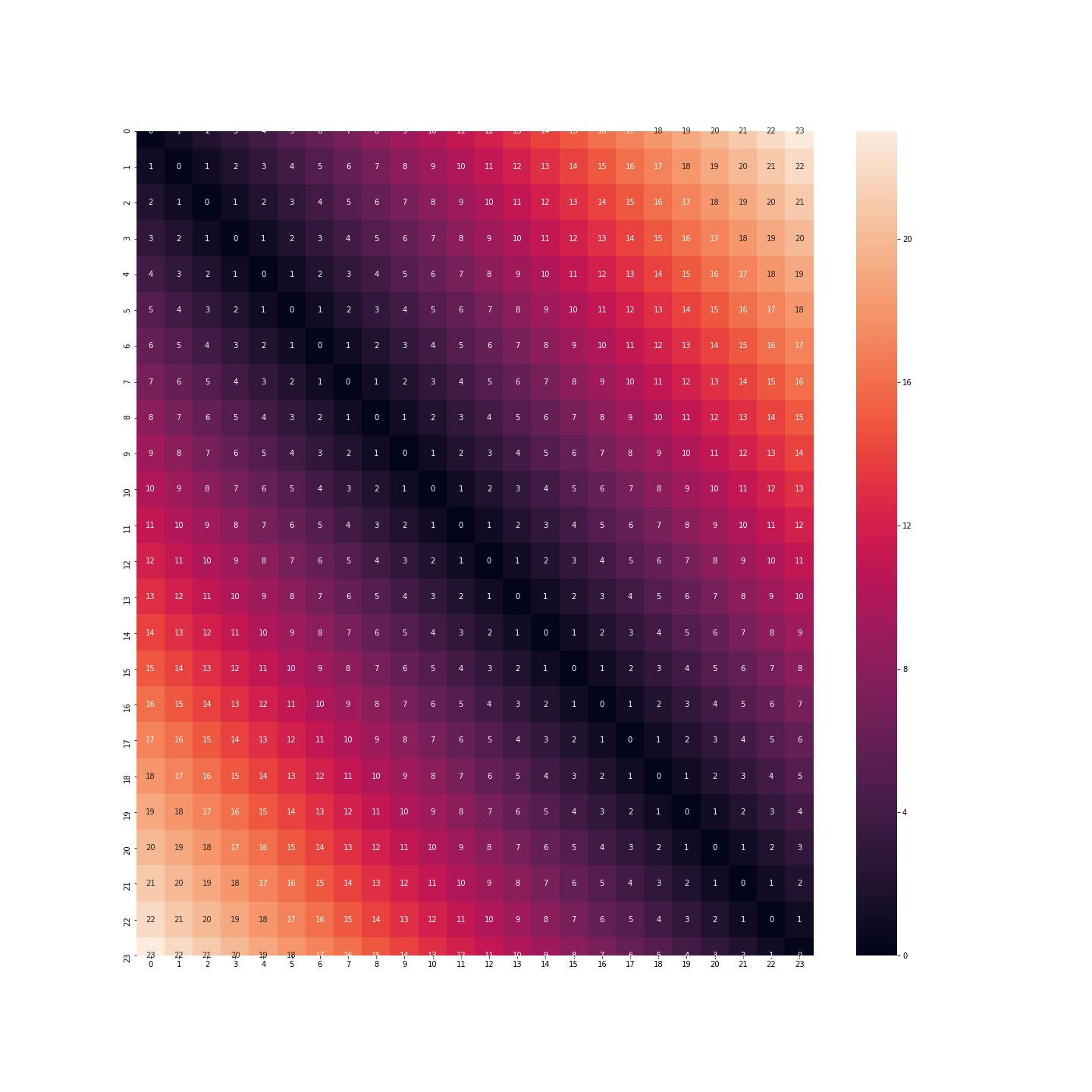
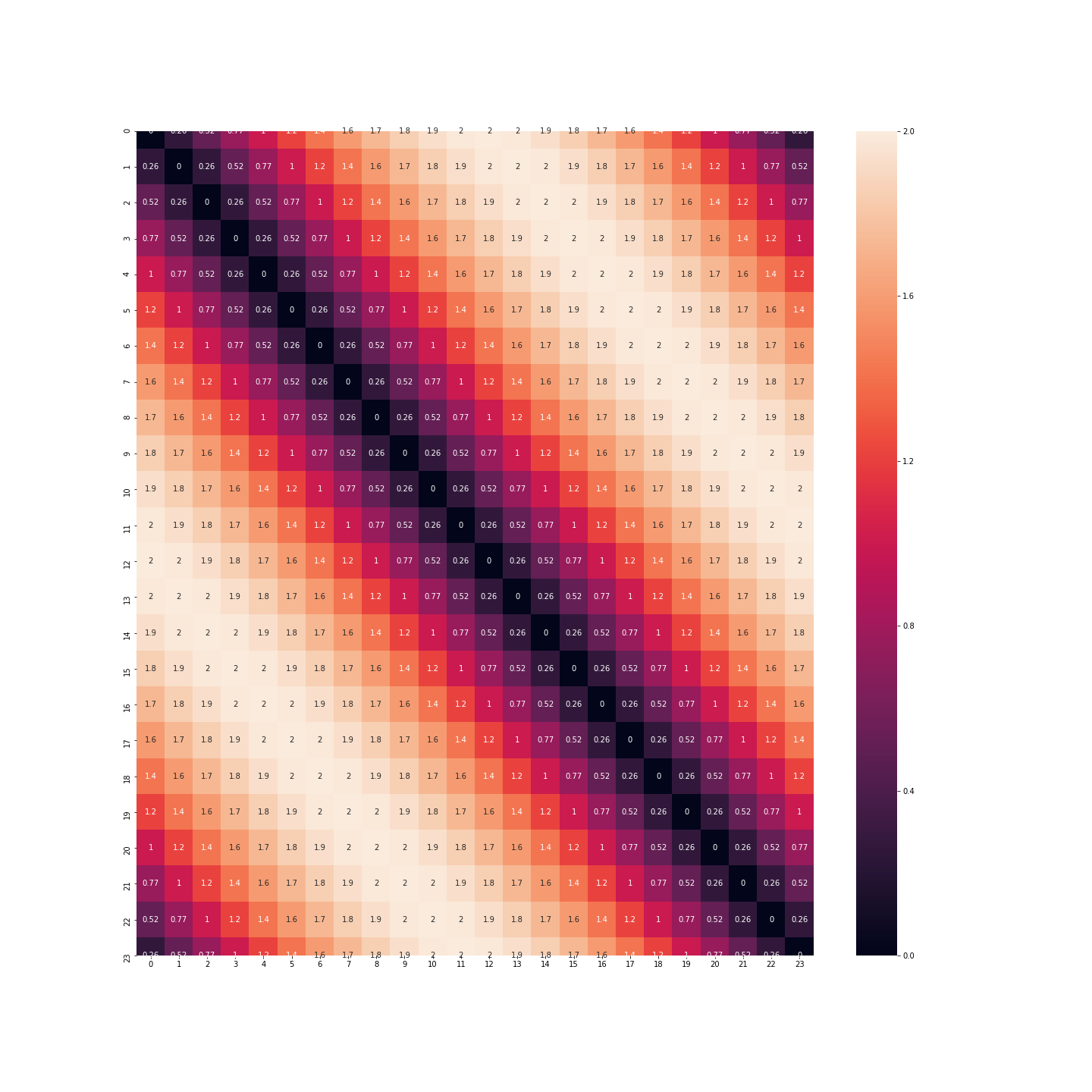
Was ist mit der Binarisierung? Diesmal haben wir nicht mehr das gleiche Problem. Der Abstand zwischen Mitternacht und 1 Uhr ist derselbe wie zwischen 23 Uhr und Mitternacht.
df_2 = df.copy(deep=True)
df_2 = pd.get_dummies(df_2, columns=['heure'])
print(df_2.head())
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_2, df_2), annot=True)
plt.show()
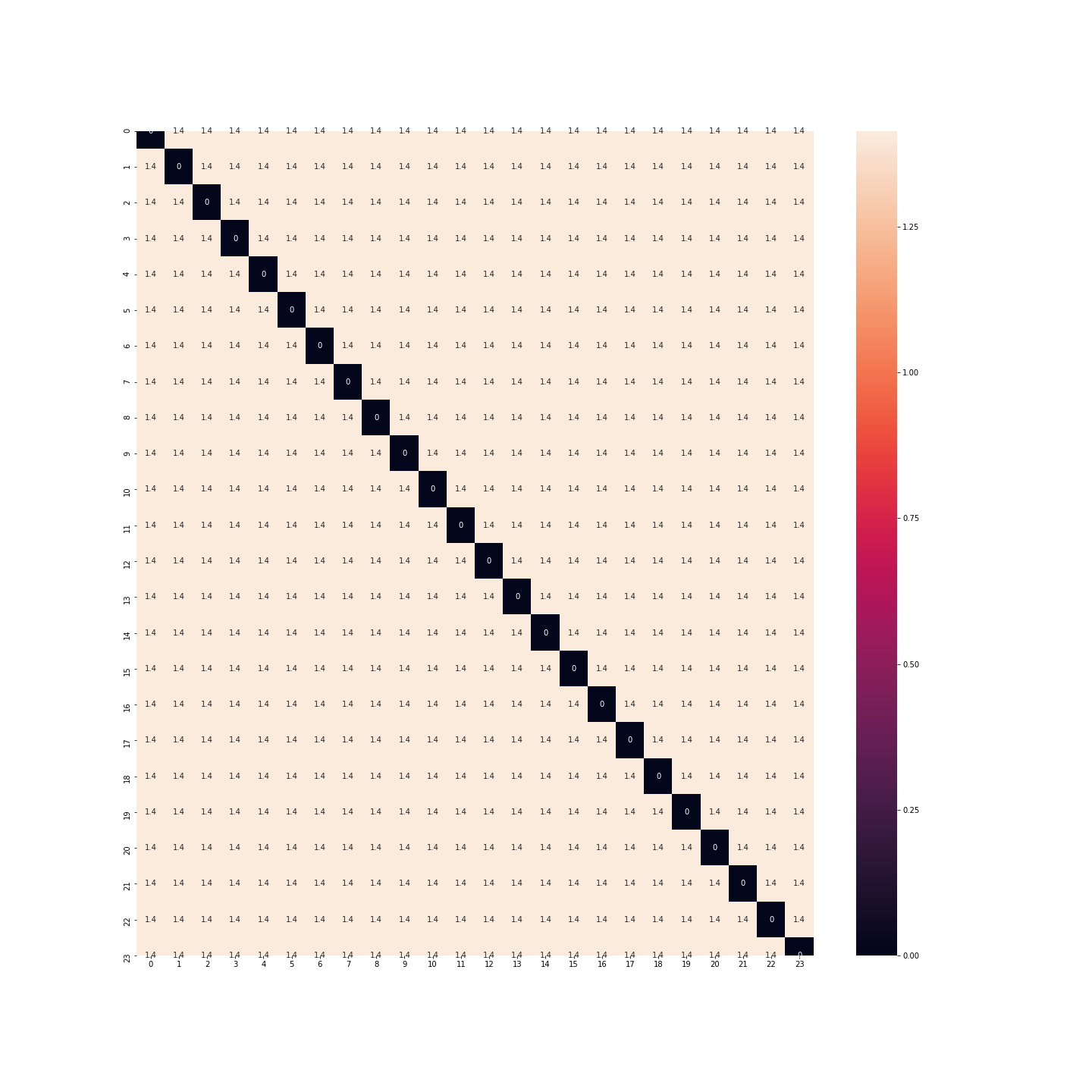
Tatsächlich sind die Abstände zwischen allen Stunden gleich… Der Abstand zwischen Mitternacht und 1 Uhr ist genauso groß wie zwischen Mitternacht und Mittag… Aber auch das ist nicht gut.
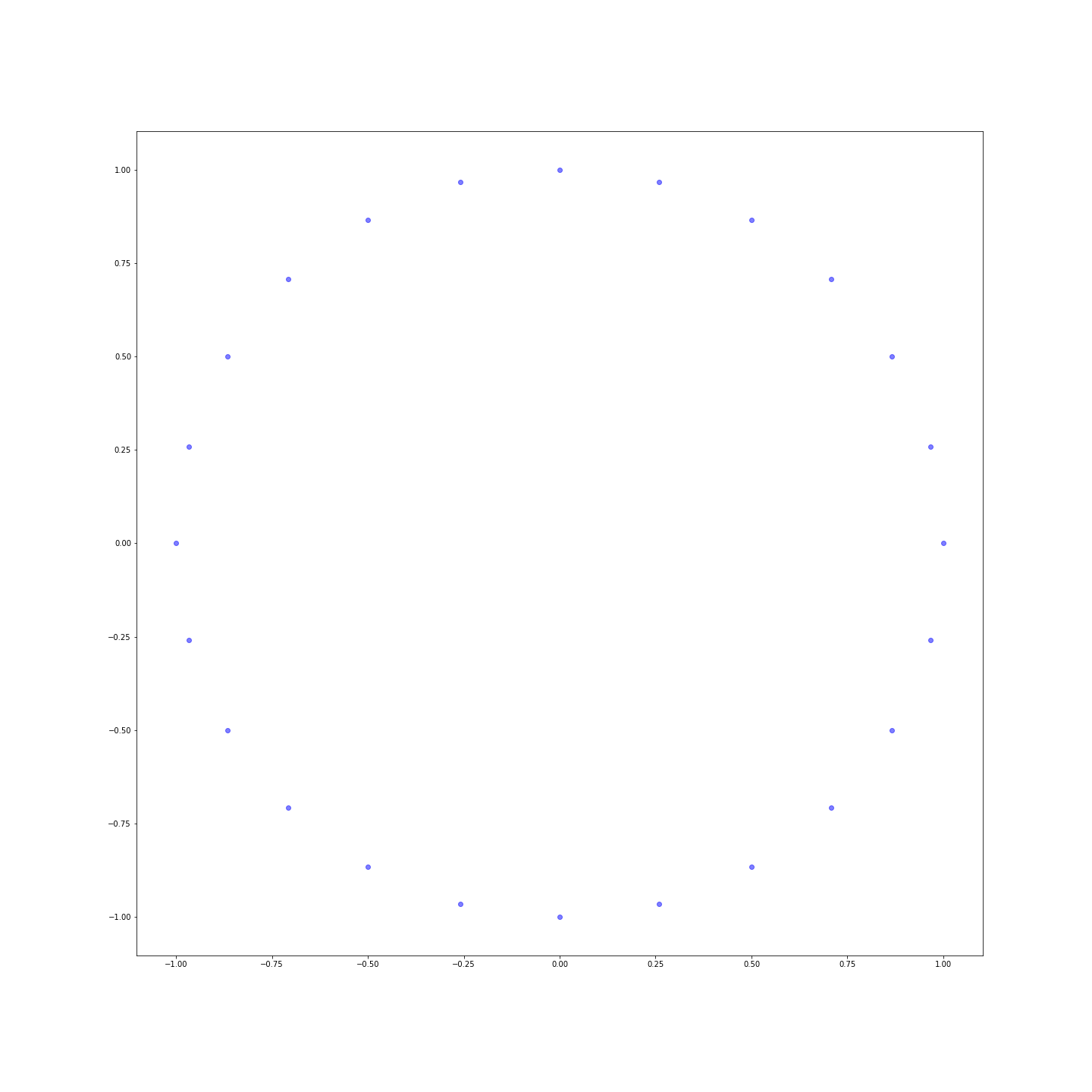
Es muss also eine andere Lösung gefunden werden. Diese andere Lösung kommt aus der Trigonometrie. Wir behalten nicht die absoluten Werte, sondern nehmen einfach den Kosinus und den Sinus dieser Werte:
df_3 = df.copy(deep=True)
df_3['sin_heure'] = df_3['heure'].apply(lambda h: np.sin(2 * np.pi * h / 24))
df_3['cos_heure'] = df_3['heure'].apply(lambda h: np.cos(2 * np.pi * h / 24))
df_3.drop(['heure'], axis=1, inplace=True)
plt.figure(figsize=(20, 20))
sns.heatmap(distance_matrix(df_3, df_3), annot=True)
plt.show()
Die Entfernungen sind viel nuancierter! Du kannst die Punkte sogar in einer Ebene darstellen, um zu sehen, dass wir gerade die Uhr neu erfunden haben:
Fazit
Dieser Schritt des Aufbaus und der Vorbereitung der Variablen unmittelbar vor dem Training eines Machine-Learning-Algorithmus ist entscheidend, da er sowohl die Algorithmen beschleunigt als auch die Ergebnisse verbessert. Die Techniken sind für die verschiedenen Variablentypen unterschiedlich, aber du solltest sie im Hinterkopf behalten, um vor der Anwendung der Algorithmen einen guten Start zu haben.
Möchtest du mehr darüber erfahren? Nimm an einer unserer nächsten Schulungen im Bootcamp- oder fortlaufenden Format teil.
Kontaktiere uns unter contact@datascientest.com oder auf Linkedin auf der DataScientest-Seite!









