La divergence de Jensen-Shannon permet de mesurer la similarité entre deux distributions de probabilité, notamment dans le domaine du Machine Learning. Découvrez tout ce que vous devez savoir sur cette mesure, de son histoire à ses applications modernes !
Au cours du XXe siècle, le mathématicien danois Johan Jensen et le statisticien américain Peter Shannon ont apporté des contributions majeures à la théorie de l’information et à la statistique.
Né en 1859, Johan Jensen a consacré une grande partie de sa carrière à l’étude des fonctions convexes et des inégalités. C’est en 1906 qu’il publie un article intitulé « Sur les fonctions convexes et les inégalités entre les valeurs moyennes ».
Il y introduit la notion de convexité, et a établi plusieurs résultats sur les inégalités de Jensen qui portent son nom. Il s’agit de résultats mathématiques décrivant les propriétés des fonctions convexes.
De son côté, Peter Shannon est né en 1917 et a longtemps étudié les mesures de divergence entre distributions de probabilité. Il a notamment travaillé sur des problèmes liés à l’estimation de la densité.
Dans les années 1940, plusieurs décennies après les travaux de Jensen, l’Américain développe des méthodes pour estimer la divergence entre distributions de probabilité.
Il se base sur la divergence de Kullback-Leibler : une mesure inventée dans les années 1950 par Solomon Kulback et Richard Leibler, largement utilisée pour quantifier la différence entre deux distributions.
Cette dernière mesure la dissimilarité entre deux distributions de probabilité en se basant sur les logarithmes des rapports de probabilité.
Plus tard, dans les années 1990, des chercheurs commencèrent à explorer les possibilités d’extensions et de variations de la divergence de Kullback-Leibler.
Leur but était de mieux prendre en compte la symétrie et la dissimilarité entre distributions. C’est ainsi qu’ils s’inspirèrent des travaux précurseurs de Johan Jensen et Peter Shannon pour créer la divergence de Jensen-Shannon.
Qu’est-ce que la divergence de Jensen-Shannon ?
La divergence de Jensen-Shannon est introduite pour la première fois dans un article de Barry E. .S. Lindgren en 1991, intitulé « Some Properties of Jensen-Shannon Divergence and Mutual Information».
Il a développé cette métrique comme une mesure de divergence symétrique entre deux distributions de probabilité. Sa principale différence avec la divergence de Kullback-Leibler qui lui sert de fondation est la symétrie.
Ainsi, elle prend la moyenne pondérée de deux divergences KL. L’une est calculée à partir de la première distribution et l’autre à partir de la deuxième.
On peut donc définir la divergence de Jensen-Shannon est définie comme la moyenne pondérée des divergences de Kullback-Leibler entre chaque distribution et une distribution moyenne.
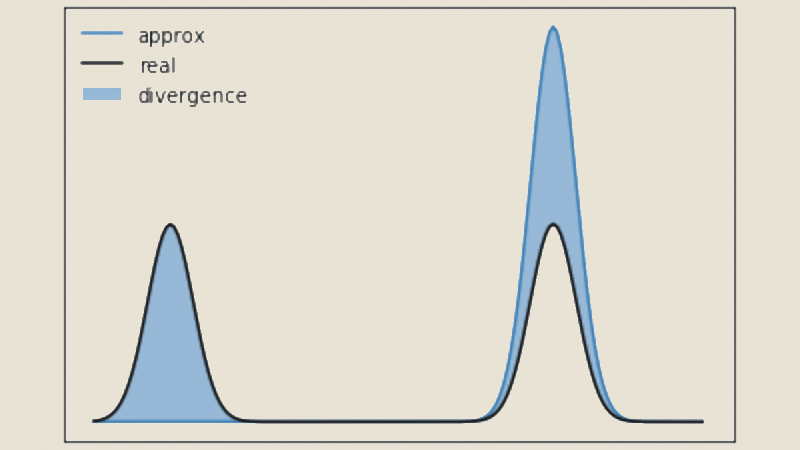
Comment calculer la divergence de Jensen-Shannon ?
La première étape pour calculer la divergence de Jensen-Shannon est de pré-traiter les données pour obtenir les distributions de probabilité P et Q.
Par la suite, les distributions de probabilité peuvent être estimées à partir des données. Il est par exemple possible de compter les occurrences de chaque élément dans l’échantillon.
Lorsque les distributions sont disponibles, on peut calculer la divergence en utilisant la formule :
JS(P || Q) = (KL(P || M) + KL(Q || M)) / 2
où M = (P + Q) / 2 et || représente l’opérateur de concaténation
Une valeur plus élevée de la divergence de JS indique une plus grande dissimilarité entre les distributions, tandis qu’une valeur plus proche de zéro indique une plus grande similarité.
Pour illustrer par un exemple concret, supposons que nous ayons deux textes et que nous voulions mesurer leur similarité.
Chaque texte peut être représenté par une distribution de mots, où chaque mot est un élément de l’alphabet.
En comptant les occurrences des mots dans chaque texte et en normalisant ces occurrences par la fréquence des totale des mots, nous obtenons les distributions de probabilité P et Q.
On utilise ensuite la formule de la divergence de Jensen-Shannon pour calculer une valeur qui indique à quel point les deux textes sont similaires !
Plusieurs propriétés importantes sont à souligner sur cette mesure. Tout d’abord, elle est toujours positive et atteint zéro si et seulement si les distributions P et Q sont identiques.
En outre, elle est bornée supérieurement par log2(n), où n est la taille de l’alphabet de la distribution. Elle est statistiquement significative et peut être utilisée dans des tests d’hypothèses et des intervalles de confiance.
Avantages et inconvénients
Le point fort de la divergence de Jensen-Shannon est la prise en compte de la structure globale des distributions. Elle est donc plus résistante aux variations locales que d’autres mesures de divergence.
Son calcul est relativement efficace, ce qui la rend par ailleurs applicable à de grandes quantités de données. Il s’agit de ses principaux avantages.
En revanche, elle peut être sensible à la taille des échantillons. Les estimations des distributions de probabilité peuvent être peu fiables en cas de petite taille, et ceci peut affecter la mesure de similarité.
Elle peut aussi être moins adaptée lorsque les distributions sont très différentes. Pour cause, elle ne capture pas les détails fins des différences locales.
Divergence de Jensen-Shannon et Machine Learning
Dans le domaine du Machine Learning, la divergence JS occupe un rôle crucial. Elle permet de mesurer la similitude entre les distributions de probabilité associées à différents échantillons ou clusters.
On peut l’utiliser pour regrouper des données similaires ensemble ou pour classifier de nouveaux échantillons en les comparant à des distributions de référence.
Dans le traitement du langage naturel, il est possible de l’utiliser pour comparer les distributions de mots dans différents textes. Ceci permet d’identifier des documents similaires, de détecter du contenu dupliqué ou de trouver des relations sémantiques entre des textes.
Il s’agit aussi d’un outil d’évaluation des modèles de langage. On peut notamment s’en servir pour évaluer la diversité et la qualité des textes générés.
En comparant les distributions de probabilité des textes générés avec celles des textes de référence, il est possible de mesurer à quel point les générations sont similaires ou différentes du corpus de référence.
Dans les cas où les données d’apprentissage et les données de test proviennent de distributions différentes, la divergence de Jensen-Shannon peut être utilisée pour guider les stratégies d’adaptation de domaine.
Cela peut aider à ajuster un modèle entraîné sur une distribution source pour mieux s’adapter aux nouvelles données d’une distribution cible.
Enfin, pour l’analyse de sentiment, la divergence JS peut être utilisée pour comparer les profils entre différents documents ou classes d’échantillons.
Cela permet d’identifier les similitudes et les différences dans l’expression, par exemple pour la détection de l’opinion ou la classification des émotions.
Divergence de Jensen-Shannon et Data Science
Pour la science des données, la divergence JS permet de comparer la similarité entre les distributions de variables ou de caractéristiques dans un ensemble de données.
Elle peut être utilisée pour mesurer la différence entre les distributions de données observées et les distributions attendues ou de référence.
Cela permet d’identifier les variations et les divergences entre les différentes distributions, ce qui peut être précieux pour la détection d’anomalies ou la validation des hypothèses.
Pour l’analyse de données textuelles, cette mesure permet d’estimer la similitude entre les distributions de mots, de phrases ou de thèmes dans des documents.
Cela peut aider à regrouper des documents similaires, à extraire des sujets communs ou à détecter des différences significatives entre les ensembles de documents.
Par exemple, elle peut être utilisée pour la classification de documents basée sur leur contenu ou pour l’analyse de sentiment en comparant les distributions de sentiments entre différents textes.
Lorsqu’il y a une grande dimensionnalité dans les données, la divergence de Jensen-Shannon peut être utilisée pour sélectionner les caractéristiques les plus discriminantes ou pour réduire la dimensionnalité des données.
En calculant la divergence entre les distributions de différentes caractéristiques, il est possible d’identifier celles qui contribuent le plus à la différenciation entre les classes ou les groupes de données.
Évaluation de modèles : Dans le processus de développement et d’évaluation des modèles prédictifs, la divergence JS peut être utilisée comme métrique pour comparer les distributions de probabilité des prédictions et des valeurs réelles.
Cela permet d’évaluer la qualité du modèle en mesurant à quel point les prédictions s’alignent sur les observations réelles. Par exemple, elle peut être utilisée dans l’évaluation des modèles de classification, de régression ou de recommandation.
Enfin, on peut l’utiliser pour mesurer la similitude entre les observations ou les instances dans un ensemble de données.
En comparant les distributions de caractéristiques entre les différentes instances, il est possible de déterminer la proximité ou la distance entre elles. Cela peut être utilisé dans des tâches de clustering pour regrouper des observations similaires ou pour effectuer des recherches de similarité dans de grandes bases de données.
Conclusion : la divergence de Jensen-Shannon, un outil clé de l’analyse de données et de l’apprentissage automatique
Depuis sa création, la divergence de Jensen-Shannon a été largement utilisée dans de nombreux domaines dont l’informatique, la statistique, le traitement du langage naturel, la bioinformatique ou le machine learning.
Il s’agit encore aujourd’hui d’un outil essentiel pour mesurer la similarité entre distributions de probabilité, qui a ouvert de nouvelles perspectives dans l’analyse de données et la modélisation statistique.
Les chercheurs du monde entier l’utilisent pour résoudre des problèmes de classification ou de clustering. C’est un élément clé de la boîte à outil des scientifiques et praticiens de nombreux domaines, à commencer par la Data Science.
Afin d’apprendre à maîtriser toutes les techniques d’analyse et de Machine Learning, vous pouvez choisir DataScientest.
Nos formations vous permettront d’acquérir toutes les compétences requises pour devenir ingénieur des données, analyste, Data Scientist, Data Product Manager ou encore ingénieur ML.
Vous découvrirez le langage Python et ses bibliothèques, les outils de DataViz, les solutions de Business Intelligence ou encore les bases de données.
Toutes nos formations s’effectuent entièrement à distance, permettent d’obtenir une certification professionnelle et sont éligibles au CPF pour le financement. Découvrez DataScientest !